ハーバード・ビジネススクールが教える 顧客サービス戦略

ハーバード・ビジネススクールが教える 顧客サービス戦略

ハーバード・ビジネススクールが教える 顧客サービス戦略

CS（Customer Satisfaction）を組織として提供するにはどうすればいいか具体的な方法を知りたいと考えて読みました。主張自体も分かりやすく、個々の主張の説明に実際の企業を事例を多数使って説明しており、読みやすかったです。良書だと思いました。

成功する顧客サービスを構成するものとして以下の4つを原則として挙げており、各章でその詳細と実践方法について説明する構成となっています。その際、複数の企業を例に紹介しているため内容も具体的かつ分かりやすかったです。

  • 原則１　「 すべてが最高」には無理がある
  • 原則２　誰かがコストを負担しなくてはならない
  • 原則３　悪いのはスタッフではない
  • 原則４　顧客をマネジメントせよ

前述の原則は普段の仕事でも意識していたことなので、非常に共感したというか、自分自身の考えはあっていたのかなという点で自信をもらえました。私自身は精神論みたいなものは持続性がないので、個人に依存せず、組織として再現性のある仕組みを作る必要があるという考え方です。また資源は有限なので、取捨選択（特にやらないことを決めるというか増やすというか）が重要という考え方です。その辺りの考え方が近い内容だったので特に違和感なく読めました。

ゼロから作るDeep Learning 5章 誤差逆伝播法

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

前回はゼロから作るDeep Learning 4章 ニューラルネットワークの学習 - n3104のブログです。

5章です。Deep Learningで有名な（？）誤差逆伝播法（Backpropagation）について学びます。4章で数値微分による勾配降下法を利用してニューラルネットワークで学習する方法について学びました。ただ、数値微分は計算コストが大きいのでより効率的に勾配を算出できる誤差逆伝播法を利用するそうで、この章ではその誤差逆伝播法の仕組みと実装方法について説明しています。

  • まえがき
    • “ひとつは「数式」によって、もうひとつは「計算グラフ(computational graph)」によって理解するというものです。前者のほうが一般的な方法で、特に、機 械学習に関する書籍の多くでは、数式を中心に話を展開していきます。確かに、数式 による説明は、厳密で簡潔になるのでもっともな方法なのですが、いきなり数式を中 心に考えようとしたら、本質的なことを見逃してしまったり、数式の羅列にとまどっ たりすることがあります。そこで本章では、計算グラフによって“視覚的”に誤差逆 伝播法を理解してもらおうと思います。実際にコードに書くことでさらに理解が深ま り「なるほど!」と納得できると思います。”
      • 計算グラフによる理解方法もあるんだー。
  • 5.2.3 連鎖律と計算グラフ
    • zの部分の偏微分を求めているのがちょっとピンとこない。。後の項で出てくるのかなー。　←　5.3.1 を見た感じ、右端も常に微分する必要はあって、今回は終端だったというだけかな。
  • 5.4 単純なレイヤの実装
  • 5.4.1 乗算レイヤの実装
    • 微分(dout)
      • これ、多分 delta out なのかなー。
        • “また、backward() の引数は、「順伝播の際の出力変数に対する微分」を入力する”
        • あってるっぽい。
  • 5.4.2 加算レイヤの実装
    • こんなに簡単に実装できるんだなー。。
  • 5.5 活性化関数レイヤの実装
    • 読めば分かるし、式変換もぎり出来た。。
    • (5.12) 式は単純に第二項は y そのもので、第三項は (1 - y) に変換できると言うだけ。
  • 5.6.1 Affine レイヤ
    • “ニューラルネットワークの順伝播で行う行列の内積は、幾何学の分野では「アフィン変換」と呼ばれます。そのため、ここでは、アフィン変換を行う処理を 「Affine レイヤ」という名前で実装していきます。”
      • なぜAffineレイヤと呼ばれるかというと行列の内積の計算がアフィン変換に含まれるからということらしい。
    • “ただし X、W、B は行列(多次元配列) であるということに注意しましょう。これまで見てきた計算グラフは「スカラ値」が ノード間を流れましたが、この例では「行列」がノード間を伝播します。”
      • そっか。ここからはノード単位からレイヤ単位に拡張されてるのか。　←　違ってた。ニューラルネットワークの場合は前のレイヤーの全ノードの出力が単一のノードの入力になるので行列に拡張されているだけだった。図3-17 入力層から第 1 層目への信号の伝達みたいな感じ。なお、行列に拡張と言ってもこの時点では W のみで、X と B はベクトルにすぎない。X が行列に拡張されるのは次節の 5.6.2 バッチ版 Affine レイヤで、そこでも B についてはベクトルのまま。
    • “(式 (5.13) が導かれる過程はここでは省略します)”
      • さすがにそろそろ導出過程は省略するようになってきたか。。
      • 導出過程はないけど、要は掛け算なので 5.4.1 乗算レイヤの実装 と同じ考え方でそれぞれ掛けるものが入れ替わり、かつ、行列なので掛ける順序が式の通りになってるって感じかなー。個々の要素を展開して数式眺めれば納得するのかなー。。
      • 式展開してたら X が横ベクトルじゃないと計算できないはずなのに W は行列で shape の値が表示されてて混乱してきた？？？
        • いろいろ調べた結果、nparray は1次元の場合はベクトルに縦とか横とかの概念がないそうで、np.transpose しても縦/横は変換されず、np.dot の場合は片方が二次元の行列でもう片方が一次元のベクトルなら縦横関係なく計算てくれることが判明した。これは補足に書いてくれてもいい気もするんだけど、3.3 多次元配列の計算 では説明してなかった。。
        • numpyの1d-arrayを2d-arrayに変換 - keisukeのブログ
          • http://kaisk.hatenadiary.com/entry/2014/09/20/185553
          • “numpyはベクトルと行列を分けているので*1，ベクトルの転置が取れなくて困る．
          • n次元ベクトルxは，numpyでは行ベクトルでも列ベクトルでもない．単にn次元ベクトル．"
        • numpy.dot — NumPy v1.12 Manual 
>>> X = np.random.rand(2)
>>> X
array([ 0.19710846,  0.80155544])
>>> W = np.random.rand(2,3)
>>> W
array([[ 0.82160224,  0.64742996,  0.16274919],
       [ 0.82007676,  0.46175103,  0.96207937]])
>>> np.dot(X, W)
array([ 0.81928174,  0.49773297,  0.8032392 ])
>>> np.dot(W, X)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shapes (2,3) and (2,) not aligned: 3 (dim 1) != 2 (dim 0)
>>> np.dot(np.transpose(W), X)
array([ 0.81928174,  0.49773297,  0.8032392 ])

# X への np.transpose は意味がない
>>> np.dot(np.transpose(X), W)
array([ 0.81928174,  0.49773297,  0.8032392 ])
>>> np.dot(np.transpose(W), np.transpose(X))
array([ 0.81928174,  0.49773297,  0.8032392 ])

# reshape して行列に変換すれば np.transpose できる
>>> X.shape
(2,)
>>> np.transpose(X).shape
(2,)
>>> X.reshape(1,2).shape
(1, 2)
>>> np.transpose(X.reshape(1,2)).shape
(2, 1)
>>> np.dot(X.reshape(1,2), W)
array([[ 0.81928174,  0.49773297,  0.8032392 ]])
>>> np.dot(np.transpose(X.reshape(1,2)), W)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shapes (2,1) and (2,3) not aligned: 1 (dim 1) != 2 (dim 0)
  • 5.6.2 バッチ版 Affine レイヤ
    • “これまで説明してきた Affine レイヤは、入力である X はひとつのデータを対象と したものでした。ここでは N 個のデータをまとめて順伝播する場合、つまり、バッ チ版の Affine レイヤを考えます”
      • ？？？ N 個のデータをまとめてというのは 5.6.1 Affine レイヤ まではレイヤではなくてやはりノードの話で、バッチ版でレイヤにまで拡張されてる？　←　これは4.2.3 ミニバッチ学習のバッチという意味だった。
  • 5.6.3 Softmax-with-Loss レイヤ
    • 図5-28 を見るとAffineもReLUもSoftmaxも全てレイヤになっている。。もうちょっと先まで読み進まないと理解できないのかなー。
    • 書いてあることは分かるんだけど、こう、なんというか納得感がないというか、結局どう使うのか分からないというか。。
    • “伝播する値をバッチの個数(batch_size)で割ることで、データ 1 個あたりの 誤差が前レイヤへ伝播する点に注意しましょう。”
      • バッチ処理なので一度に複数のデータを処理するので1回のバッチの変化量のオーダーを揃えようとしてるでいいんだっけ？
      • 4.2.3 ミニバッチ学習 に書かれているとおりで、"ただし、最後に N で割って正規化しています。こ の N で割ることによって、1 個あたりの「平均の損失関数」を求めることになりま す。そのように平均化すれば、訓練データの数に関係なく、いつでも統一した指標が 得られます。たとえば、訓練データが 1,000 個や 10,000 個の場合であっても、1 個 あたりの平均の損失関数を求められます。"だかららしい。ここは式 (4.3) だけなら納得なんだけど、SoftmaxWithLoss の実装では損失を合計してないんだよなー。。
      • 4.5 学習アルゴリズムの実装 に書かれているように1回の学習で更新するパラメータのオーダーをバッチサイズに関係なく一定にするってことかなー。。
      • 合計のオーダーを揃えようとしてるでいいみたい。合計する箇所はAffineレイヤだった。5.6.2 バッチ版 Affine レイヤ の 図5-27 バッチ版 Affine レイヤの計算グラフ を見ると分かるが、W については内積なのでバッチの個数分、つまり N 個が足される。なので、あらかじめ batch_size つまり N で割っておくとオーダーが揃うことになる。実装は 5.7 誤差逆伝播法の実装 の train_neuralnet.py で確認できる。ここで batch_size を減らすと N が変わることを layers.py でデバッグプリント入れると確認できる。

train_neuralnet.py

# batch_size = 100
batch_size = 3

layers.py

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        # 以下、追加したデバッグプリント
        print(self.x.T.shape)
        print(dout.shape)
        print(self.dW.shape)
        self.db = np.sum(dout, axis=0)

出力

(50, 3)
(3, 10)
(50, 10)
(784, 3)
(3, 50)
(784, 50)
  • 5.7 誤差逆伝播法の実装
    • この節で今まで出てきたものの全体における位置づけが分かるっぽい。
  • 5.7.1 ニューラルネットワークの学習の全体図
    • “これまで説明した誤差逆伝播法が登場するのは、ステップ 2 の「勾配の算出」で す。前章では、この勾配を求めるために数値微分を利用しましたが、数値微分は簡単 に実装できる反面、計算に多くの時間がかかりました。誤差逆伝播法を用いれば、時 間を要する数値微分とは違い、高速に効率良く勾配を求めることができます。”
      • なるほど。結局勾配を求める際の計算の効率化が目的なのか。
  • 5.7.2 誤差逆伝播法に対応したニューラルネットワークの 実装
    • self.params[‘b1’] = np.zeros(hidden_size)
      • バイアス項は初期値 0 で初期化するのかー。
    • self.layers = OrderedDict()
      • 本文にも開設のあるとおり順番付きディクショナリらしい。
      • Python本体に含まれている模様。
      • Javaで言うとこの LinkedHashMap みたいなものか。
    • self.layers[‘Relu1’] = Relu()
      • Relu は 5.5.1 ReLU レイヤ で実装していて、ノードかレイヤか分からなかったが、よくよく見直したらレイヤとして実装されてた。なるほど。そして、Relu レイヤは活性化関数のレイヤなのでプログラミングとしてはニューラルネットワークの1つの層を2つのレイヤ（AffineとRelu）で実装してるってことか。
      • 5.4 単純なレイヤの実装 についても改めて見てみたが、こちらはノードを実現するためのレイヤで合ってた。
        • “計算グラフの乗算ノードを「乗算レイヤ(MulLayer)」、加算ノー ドを「加算レイヤ(AddLayer)」という名前で実装することにします。”
      • レイヤという用語は単なる層ではあるが、ニューラルネットワークとしてのレイヤと計算を行うレイヤ（単ノード/複数ノード）があるので、何というか用語の使い分けなりがあっても良かった気はする。　←　改めて読み直したらいちおう説明はしていた。うーん。。
        • 5.4 単純なレイヤの実装 の最初に断り書きはあった。
          • “ここで言う「レイヤ」とは、ニューラルネットワー クにおける機能の単位です。たとえば、シグモイド関数のための Sigmoid や、 行列の内積のための Affine など、レイヤ単位で実装を行います。そのため、 ここでも「レイヤ」という単位で、乗算ノードと加算ノードを実装します。”
        • 5.5 活性化関数レイヤの実装 の最初でも以下のように層としてのレイヤと記述してはいた。
          • “ここでは、ニューラルネットワークを構成する「層(レイヤ)」をひとつのクラ スとして実装することにします。まずは、活性化関数である ReLU と Sigmoid レイ ヤを実装していきます。”
    • self.lastLayer = SoftmaxWithLoss()
      • predict メソッドでは利用しない。これは 5.6.3 Softmax-with-Loss レイヤ に書いてある。
        • “ニューラルネットワークで行う処理には、推論(inference)と学習の 2 つの フェーズがあります。ニューラルネットワークの推論では、通常、Softmax レ イヤは使用しません。たとえば、図5-28 のネットワークで推論を行う場合、 最後の Affine レイヤの出力を認識結果として用います。なお、ニューラルネットワークの正規化しない出力結果(図5-28 では Softmax の前層の Affine レ イヤの出力)は、「スコア」と呼ぶことがあります。つまり、ニューラルネット ワークの推論で答えをひとつだけ出す場合は、スコアの最大値だけに興味があ るため、Softmax レイヤは必要ない、ということです。一方、ニューラルネッ トワークの学習時には、Softmax レイヤが必要になります。”
    • 実際に動かして動作を確認するには 5.7.4 誤差逆伝播法を使った学習 で登場する train_neuralnet.py を利用する。
  • 5.7.3 誤差逆伝播法の勾配確認
    • “さて、数値微分は計算に時間がかかります。そして、誤差逆伝播法の(正しい)実 装があれば、数値微分の実装は必要ありません。そうであれば、数値微分は何の役に 立つのでしょうか? 実は、数値微分が実践的に必要とされるのは、誤差逆伝播法の 実装の正しさを確認する場面なのです。数値微分の利点は、実装が簡単であるということです。そのため、数値微分の実装 はミスが起きにくく、一方、誤差逆伝播法の実装は複雑になるためミスが起きやすいの が一般的です。そこで、数値微分の結果と誤差逆伝播法の結果を比較して、誤差逆伝 播法の実装の正しさを確認することがよく行われます。”
      • なるほどなー。
    • 数値微分は計算に時間が掛かるということだったけど、確かに数値微分はパラメータ毎の勾配を求めるためにはネットワーク全体を2回順伝播することになるのに対して、誤差逆伝播法の場合は順伝播と逆伝播の合計 2 回だけで演算終わるもんなー。なので、数値微分自体の計算が重いというよりは、数値微分の場合はレイヤ数に比例して計算量が増えるので重いと言った方が適切なんだろうな。
    • x_batch = x_train[:3] 
>>> x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> x[:3]
array([0, 1, 2])
>>> y = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y[:3]
[0, 1, 2]

5章については最初はレイヤの定義が曖昧に見えて悩みました。結局最後まで読み進めた上でソースにデバッグプリント入れながら動きを確認することで、最終的には理解できてとてもスッキリしました。また4章までの部分も何度か読み直したので、5章は4章までを理解していないと読んでいてスッキリしないかもしれません。

次回はゼロから作るDeep Learning 6章 学習に関するテクニック - n3104のブログです。

プラットフォーム ブランディング

プラットフォーム ブランディング

プラットフォーム ブランディング

IoTの成功事例、コマツの「KOMTRAX」は何がすごいのか : 市況かぶ全力２階建を偶然読んでいた際に紹介されていたので読んでみました。ブランド戦略について体系立てて説明しており、実践における留意点も紹介されていて良書だと思いました。

プラットフォームというと仕事柄身近なのはアマゾン（AWS）やアップル（iOS）だったりするんですが、コマツのKOMTRAXも確かにプラットフォームだと思ったので、そういうプラットフォームの作り方とか仕組みが書いてあるかなと期待して読んでみました。実際にはブランド戦略が主題で、プラットフォームについてはあくまでもブランド戦略の要素として紹介していました。なお、コマツのKOMTRAXについては10行程度しか書かれてませんでしたｗ

あとがきにも書かれている通りもともとブランディングに関わっている現場担当者向けではなく、（ブランド戦略に理解の浅い）経営者向けに書かれているということもあり、ブランド戦略に登場する概念について基本的な定義から個々の事例の分析、実践方法から歴史まで紹介してくれていて読みやすかったです。また、それぞれのテーマについて深掘りするための書籍も紹介しており、まずはこの本を読んで全体像を掴み、その上で個別のテーマを学ぶのが効率がよさそうに思いました。

本書でも触れられていることですが、色々なものがコモディティ化する中で、ブランド戦略による差別化は必須の要素になってるんだなーと実感しました。今後、仕事において色々考える際に役に立ちそうな印象を持ちました。

ゼロから作るDeep Learning 4章 ニューラルネットワークの学習

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

前回はゼロから作るDeep Learning 3章 ニューラルネットワーク - n3104のブログです。

4章です。3章では学習済みのモデルを使いましたが、4章ではそのモデルの学習方法について学びます。といっても、実際にニューラルネットワークで学習する際は4章で学ぶ数値微分ではなく5章で学ぶ誤差逆伝播法を利用します。なので、モデルの学習方法というよりはモデルを学習する仕組みについて学ぶと言ったほうが適切かもです。

  • 4.1.1 データ駆動
    • “機械学習はデータが命です。”
      • ほんとその通り。
    • もちろん特徴量の抽出は考えなくて良くなるという建前だけど、元のデータが役に立つ情報を含んでいなければ当然いけないし、ネットワークの設計は残ると思うのだけど。。
      • 画像の識別なら同じネットワークが使えるのかなー。でも、画層の種類は問題によって異なるだろうし、画像の大きさとか階調でも違う気がするんだけど。。
  • 4.2 損失関数
    • 4.1.2 訓練データとテストデータでの汎化能力の説明にあるように1節で1つの概念を説明するようにする構成はとてもいいと思うんだけど、「幸せ指標」はメタファとしてはイケてない気が。。テストの点数ぐらいで良かった気がするんだけどｗ
  • 4.2.2 交差エントロピー誤差
    • 2 乗和誤差と比べて交差エントロピー誤差はクラスラベルの次元のみ利用するから、分類問題にしか使えないんだろうなー。その分、はっきりと結果が出るんだろうけど。
    • y = logxのグラフで 0 - 1 の区間は -inf - 0 に対応してるから -log すると 0 - inf になるって言うわけかー。
    • “中身の実装では、np.log の 計算時に、微小な値である delta を足して計算しています。これは、np.log(0) の ような計算が発生した場合、np.log(0) はマイナスの無限大を表す-inf となり、そ うなってしまうと、それ以上計算を進めることができなくなります。その防止策とし て、微小な値を追加して、マイナス無限大を発生させないようにしています。”
      • なるほどー。プログラムとして実装する上でのノウハウだなー。
      • delta = 1e-7 となってるけど e-7 が妥当というのはどこから来てるんだろう？
  • 4.2.3 ミニバッチ学習
    • “ただし、最後に N で割って正規化しています。こ の N で割ることによって、1 個あたりの「平均の損失関数」を求めることになりま す。そのように平均化すれば、訓練データの数に関係なく、いつでも統一した指標が 得られます。たとえば、訓練データが 1,000 個や 10,000 個の場合であっても、1 個 あたりの平均の損失関数を求められます。”
      • なるほど。
  • 4.2.4 [バッチ対応版]交差エントロピー誤差の実装
    • cross_entropy_error 関数は分かりやすくするためだろうが delta によるエラー回避のコードが省略されているので、実際に実行するとエラーになったｗ
    • ndim は配列の次元数だった。
    • reshape を使うことで配列の次元数を変換することも可能。なのでここでは入力が一次元配列の場合に二次元配列に変換している。
    • y.shape[0] はレコード数になる。
    • np.log( y[np.arange(batch_size), t] ) の所は正解ラベルが配列のインデックスと一致するラベル名だから動作するわけであって、他のラベルだと動作しないのだから紹介するのはどうなんだろう。。　←　[2017-04-20 追記] 一般的にエンコードするから問題なかった。

ndimについて

>>> np.array([1, 2]).ndim
1
>>> np.array([1, 2]).shape
(2,)
>>> np.array([[1, 2],[3,4]]).ndim
2
>>> np.array([[1, 2],[3,4]]).shape
(2, 2)
>>> np.array([[1, 2],[3,4]]).reshape(4,1)
array([[1],
       [2],
       [3],
       [4]])
>>> np.array([[1, 2],[3,4]]).reshape(1,4)
array([[1, 2, 3, 4]])
>>> np.array([[1, 2],[3,4]]).reshape(1,4).ndim
2
>>> np.array([[1, 2],[3,4]]).reshape(4,1).ndim
2
>>> np.array([[1, 2],[3,4]]).reshape(4)
array([1, 2, 3, 4])

y[np.arange(batch_size), t] について

>>> # 3行分のダミーデータを作る。
... y = softmax(np.random.rand(3, 10))
>>> y
array([[ 0.07759622,  0.08309147,  0.09904634,  0.07516991,  0.06775452,
         0.13294043,  0.11345575,  0.07123801,  0.150684  ,  0.12902336],
       [ 0.10928588,  0.09100464,  0.09566815,  0.05923705,  0.0791873 ,
         0.08125782,  0.13062538,  0.08983766,  0.14875257,  0.11514354],
       [ 0.10586304,  0.13518227,  0.1316193 ,  0.12738668,  0.06843716,
         0.05849982,  0.13193427,  0.11540083,  0.05508124,  0.07059538]])
>>>
>>> t = np.array([2, 5, 7])
>>> batch_size = y.shape[0]
>>> # [0, 2], [1, 5], [2, 7] のデータが抽出されることが分かる。
... y[np.arange(batch_size), t]
array([ 0.09904634,  0.08125782,  0.11540083])
>>>
>>> y[0, 2]
0.099046337771526632
>>> y[1, 5]
0.081257822450627418
>>> y[2, 7]
0.11540082864090417
  • 4.2.5 なぜ損失関数を設定するのか?
    • “「認識精度」を指標にすべきではないか”
      • 実際に認識精度を指標としてパラメータのチューニングってできるんだっけ？
    • “ニューラルネットワークの学習の際に、認識精度を“指標”にしてはいけない。 その理由は、認識精度を指標にすると、パラメータの微分がほとんどの場所で 0 になってしまうからである。”
      • “つまり、パラメータの少しの調整だけでは、認識 精度は改善されず一定のままなのです。もし認識精度が改善されたとしても、その値 は 32.0123…% のような連続的な変化ではなく、33% や 34% のように、不連続のと びとびの値へと変わってしまいます。一方、損失関数を指標とした場合、現在の損失 関数の値は 0.92543…のような値によって表されます。そして、パラメータの値を少 し変化させると、それに反応して損失関数も 0.93432…のように連続的に変化するの です。 ”
      • 書いてあることはその通りなんだろうけど、いまいち腑に落ちないなー。
    • “活性化関数の「ステップ関 数」にも同じ話が当てはまります。”
      • “ステップ関数は「ししおどし」のように、ある瞬間だけ変化を起こす関数でした が、一方、シグモイド関数の微分(接線)は、図4-4 に示すように、出力(縦軸の値) が連続的に変化し、さらに、曲線の傾きも連続的に変化します。つまり、シグモイド 関数の微分はどの場所であっても 0 にはならないのです。これは、ニューラルネット ワークの「学習」において重要な性質になります。この性質――傾きが 0 にはならな い――によって、ニューラルネットワークは正しい学習が行えるようになります。”
      • ここはわりと腑に落ちた。要は極端になるってことなのかなー。。
  • 4.3.1 微分
    • “ここで行っているように、微小な差分によって微分を求めることを数値微分 (numerical differentiation)と言います。一方、数式の展開によって微分を求めることは、解析的(analytic)という言葉を用いて、たとえば、「解析的に 解く」とか「解析的に微分を求める」などと言います。たとえば、y = x2 の微 分は、解析的には、dy = 2x として解くことができます。”
    • 数値微分は中心差分を使うだけでいいんだ。なんて単純なんだ。。！
    • 実際に前方差分のみと中心差分の場合とで比べてみたら、前方差分のみは 0 になってしまったｗ
def numerical_diff1(f, x):
    h = 10e-50
    return (f(x+h) - f(x)) / h


def numerical_diff2(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)


def function_1(x):
    return 0.01*x**2 + 0.1*x


print(numerical_diff1(function_1, 5))
print(numerical_diff1(function_1, 10))
print(numerical_diff2(function_1, 5))
print(numerical_diff2(function_1, 10))

出力

0.0
0.0
0.1999999999990898
0.2999999999986347
  • 4.3.2 数値微分の例
    • 4.3.1 微分 を確認する際に少し読んでいたので特に気になる点はなかった。
  • 4.3.3 偏微分
    • 説明は分かるんだけど、初めて偏微分見た人は理解が追いつくのかな。。
    • 特に説明してないけど、numerical_diff を使って偏微分を実装している。これで偏微分が出来るのは偏微分する変数以外は定数になってるからだよなー。結果的に偏微分の対象となる変数の微分、つまり微小な変化の極限が出てる。
  • 4.4 勾配
    • “すべての変数の偏微分をベクトルとしてまとめた ものを勾配(gradient)と言います。”
      • そうだったのか！
    • “ひとつ補足として述べるとすれ ば、np.zeros_like(x) は、x と同じ形状の配列で、その要素がすべて 0 の配列を 生成するということです。”
      • いや、そこよりも色々補足必要な気がするｗ
      • numerical_gradient で勾配が出せるのは、次元毎に中心差分を取ってるから。要は numerical_diff のロジックを再実装している。対象となる次元以外の次元は同じ値になるので結果的に相殺され、対象となる次元の微分、つまり偏微分を出せる。
      • 引数となる x に再代入しているけれど、最後に tmp_val を代入しているのでもとに戻る。とはいえ、処理中に例外発生したら呼び出し元の配列の中身が書き換わるから、この実装方法は結構微妙な気がするんだけど。。機械学習の場合は巨大な行列を扱うこともあるからメモリ節約の観点でわざわざコピーせずにやるのかなー？
    • “この勾配は何を意味しているのでしょうか? そ れを理解するために、f (x0 , x1 ) = x20 + x21 の勾配を図で表してみることにしましょ う。ただし、ここでは勾配の結果にマイナスを付けたベクトルを描画します”
      • マイナスつけてるなら納得。
    • “勾配が示す方向は、各場所において関数の値を最も減らす方向”
      • マイナス付けた場合という但し書きはあってもいい気もするが。要は傾きなので単純な勾配は減らす方向にならない。
  • 4.4.1 勾配法
    • “また、関数が複雑で歪な形をしていると、(ほとんど)平らな土地に入 り込み、「プラトー」と呼ばれる学習が進まない停滞期に陥ることがあります。”
      • なるほどー。確かにこういうケースもありそう。
    • “勾配法は、目的が最小値を探すことか、それとも最大値を探すことかによって 呼び名が変わります。正確には、最小値を探す場合を勾配降下法(gradient descent method)、最大値を探す場合を勾配上昇法(gradient ascent method)と言います。ただし、損失関数の符号を反転させれば、最小値を探す 問題と最大値を探す問題は同じことになるので、「降下」か「上昇」かの違いは 本質的には重要ではありません。一般的に、ニューラルネットワーク(ディー プラーニング)の分野では、勾配法は「勾配降下法」として登場することが多 くあります。 ”
      • 勾配上昇法というものあるんだねー。でも、上昇法だと無限を目指す必要があるから降下法を使うのかなー。　←　[2017-05-19 追記] そういう意味ではなくて上に凸なら勾配上昇法で下に凸なら勾配降下法というだけだった。そもそも、下に凸でもそこが 0 とは限らず、どこまで深いかは関数次第。
    • “ニューラルネットワークの学習においては、学習率の値を変更し ながら、正しく学習できているかどうか、確認作業を行うのが一般的です。”
      • 学習率というハイパーパラメーターも残ってたか。。
      • “学習率のようなパラメータはハイパーパラメータと言います。これは、ニュー ラルネットワークのパラメータ――重みやバイアス――とは性質の異なるパラ メータです。なぜなら、ニューラルネットワークの重みパラメータは訓練デー タと学習アルゴリズムによって“自動”で獲得されるパラメータであるのに対し て、学習率のようなハイパーパラメータは人の手によって設定されるパラメー タだからです。一般的には、このハイパーパラメータをいろいろな値で試しな がら、うまく学習できるケースを探すという作業が必要になります。 ”
    • gradient_method.py はカレントディレクトリが ch04 であることを前提としていた。これをIntelliJでやる手順は以下の通り。
      • File -> Project Structure… (Cmd+;)
      • Modules -> Sources タブで ch01…ch08 を選択状態にして Sources ボタンで追加
    • “この実験の結果が示すように、学習率が大きすぎると、大きな値へと発散してしま います。逆に、学習率が小さすぎると、ほとんど更新されずに終わってしまいます。”
      • gradient_descent 関数は init_x の中身を書き換える実装になってた。なので、実際は書き換えない実装にしないと駄目な気もするけど、機械学習の界隈ではそういう割り切りなのかなー。
      • 実際にいくつか試したが、今回だと 1.0 を超えると大きすぎて発散していく。
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
from gradient_2d import numerical_gradient


def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)


def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])    

lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)

plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
print(init_x)

init_x = np.array([3.0, 4.0])
lr = 0.95
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot(x_history[:,0], x_history[:,1], 'o')
print(init_x)

init_x = np.array([3.0, -4.0])
lr = 0.01
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot(x_history[:,0], x_history[:,1], 'o')
print(init_x)

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlim(-5.5, 5.5)
plt.ylim(-5.5, 5.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()

f:id:n-3104:20170320165206p:plain

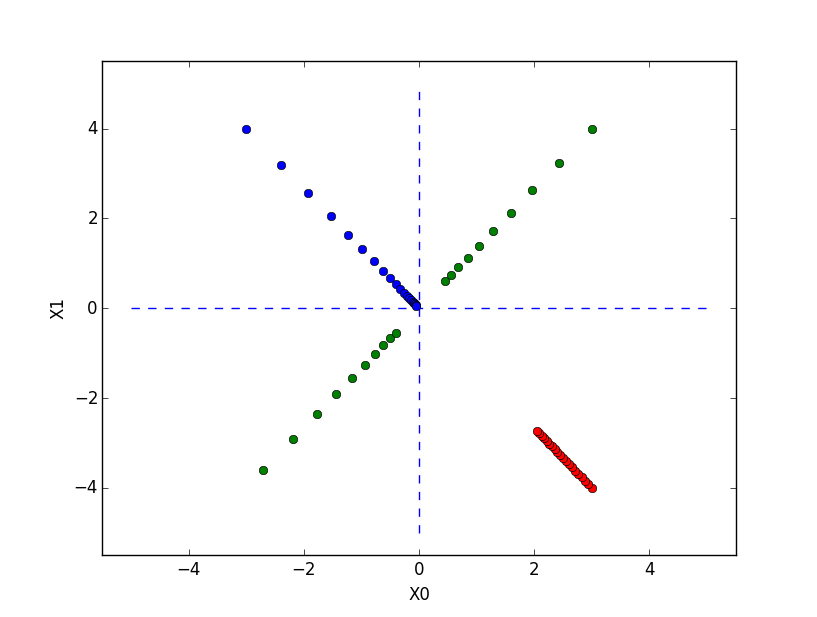
  • 4.4.2 ニューラルネットワークに対する勾配
    • 項のタイトル通り、本当に勾配を1回出すだけで、学習しない。1項1テーマに絞ってるな、ほんと。
    • ネットワークの形は図示したほうがいい気がするけど、それは次節以降で表記してるのかなー。結局、何を求めたかイメージわかない人もいるのでは。
      • 最後まで確認したが、4章の範囲ではネットワークの形は図示しないんだなー。
    • W は np.random.randn で生成しているので、当然毎回結果が異なるｗとはいえ、x と t は固定だからある程度傾向は似るんだねー。
    • 一通りコードを追いかけ直したけど、ここのサンプルソースはすごい分かりにくいのでは。。普通に f の引数 W を利用する損失関数にした方が直感出来だった気がする。
      • W に関する勾配を出すわけだから損失関数は W に関する関数である必要がある。で、loss 関数は内部で predict 関数を実行するので、結果的に loss 関数は W に関する関数であると言える。なので、勾配自体は出せる。
        • numerical_gradient 関数で勾配が出せるのは、第2引数が net.W だから。そのため、predict 関数で利用する W の参照が得られるので、numerical_gradient 関数内で前方差分と後方差分を出す際に W の参照を経由して微小量 h が増減する。。
        • “(ここで定義した f(W) という関数の引数 W は、ダミーとし て設けたものです。これは、numerical_gradient(f, x) が内部で f(x) を実行す るため、それと整合性がとれるように f(W) を定義しました)”
          • そうではなくて、ここで net.W を渡さないとそもそも W を変化させて損失関数 f を実行できないから勾配が取得できない。ここは、途中で筆者が混乱したのかなー。simpleNet のコンストラクタで W を指定するのではなくて、predict と loss 関数の引数に W があってもいい気がするんだけど。まぁ、そのなるとクラスにする意味もなくなるけどねー。。
            • ここについては、ほんとにダミーでもよかった。4.5.1 で self.params でアクセスしてた。。。
  • 4.5 学習アルゴリズムの実装
    • 学習について分かりやすくまとまっている。ただ、機械学習について初めてこの本で学ぶ人はどこまで理解できるんだろう。。
  • 4.5.1 2 層ニューラルネットワークのクラス
    • numerical_gradient を見てて思うが、こういう感じで勾配というか W と b の偏微分出せちゃうんだねー。。実際、loss 関数の中で predict 関数を呼び出していて、その中で y を出すために W と b を使って何度か計算してるけど、これを1つの数式にできちゃうもんなー。で、それぞれの偏微分ができちゃうと考えると、確かに数学そこまで分からなくてもコードレベルで理解できるというか、こう書けばいいというのはわかるなー。。
    • 今後 gradient 関数を使うし、numerical_gradient だと計算が遅いからといって、若干天下り的な感じもするねｗ
    • t = np.random.rand(100, 10) # ダミーの正解ラベル(100 枚分)
      • これ、正解ラベル自体が確率分布っぽくなっちゃうけど、それは問題ないんだっけ？
        • MNISTのデータは1つだけ 1 で他は 0 だった。だよねー。。
>>> np.random.rand(3, 10)
array([[ 0.65365022,  0.63623433,  0.70117989,  0.89724433,  0.82817134,
         0.31230608,  0.34446204,  0.23931909,  0.13342318,  0.67355462],
       [ 0.85156144,  0.10901498,  0.02327781,  0.69283457,  0.13562442,
         0.09658677,  0.32591785,  0.00592776,  0.38647803,  0.91804246],
       [ 0.86498541,  0.03354259,  0.69663751,  0.01011192,  0.1069335 ,
         0.30273103,  0.8269463 ,  0.4885381 ,  0.20540422,  0.9368264 ]])
  • 4.5.2 ミニバッチ学習の実装
    • train_neuralnet.py のソースが描画するグラフは loss ではなくて訓練データとテストデータの正解率の推移だったｗ
      • loss を表示するようにコードを書いてみたけど、最初から loss の値は 2 ぐらいからスタートしてた。書籍中のグラフはどこから持ってきたｗ？
  • 4.5.3 テストデータで評価
    • “エポック(epoch)とは単位を表します。1 エポックとは学習において訓練 データをすべて使い切ったときの回数に対応します。たとえば、10,000 個の 訓練データに対して 100 個のミニバッチで学習する場合、確率的勾配降下法を 100 回繰り返したら、すべての訓練データを“見た”ことになります。この場 合、100 回= 1 エポックとなります。”
      • 分かりやすい。要は訓練データを一通り学習し終えたら1エポック。で、イテレーション数自体はエポックというか訓練データのサイズは考慮しないでバッチサイズと一緒に指定するっぽい。言われてみると、いままでもそんな感じだったかも。
    • train_neuralnet.py は 4.5.3 のソースということか。

個人的には数値微分の実装で興奮しました。こんな簡単に実装できるんですね！

次回はゼロから作るDeep Learning 5章 誤差逆伝播法 - n3104のブログです。

ゼロから作るDeep Learning 3章 ニューラルネットワーク

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

前回はゼロから作るDeep Learning 2章 パーセプトロン - n3104のブログです。

最近やっと5章まで読み終わりました。前回からだいぶ時間が空いてしまいましたが3章のメモをブログにしました。ついに実際に予測します。といっても学習済みのモデルを使いますけどもｗ

  • 3.1.3 活性化関数の登場
    • 図 3 - 4 活性化関数によるプロセスを明示的に図示する
      • すごい分かりやすい！
    • “「パーセプトロン」という言葉が指すアルゴリズムは、本書では厳密な統一がな されずに使われています。一般的に、「単純パーセプトロン」といえば、それは 単層のネットワークで、活性化関数にステップ関数(閾値を境にして出力が切り 替わる関数)を使用したモデルを指します。「多層パーセプトロン」というと、 それはニューラルネットワーク――多層で、シグモイド関数などの滑らかな活 性化関数を使用するネットワーク――を指すのが一般的です。 ”
      • なるほど。
  • 3.2 活性化関数
    • “つまり、活性化 関数の候補としてたくさんある関数の中で、パーセプトロンは「ステップ関数」を採 用しているのです。パーセプトロンでは活性化関数にステップ関数を用いているなら ば、活性化関数にステップ関数以外の関数を使ったらどうなるのでしょうか? 実は、 活性化関数をステップ関数から別の関数に変更することで、ニューラルネットワーク の世界へと進むことができるのです! ”
      • なるほど。この本は概念の説明が丁寧で分かりやすいなー。
  • 3.2.3 ステップ関数のグラフ
    • plt.ylim(-0.1, 1.1) を指定しないとy軸が0-1となり、グラフがただの直線になってしまうｗ　なので、上下に余分に 0.1 ずつ広いy軸にしている模様。
  • 3.2.4 シグモイド関数の実装
    • “シグモイド関数の実装が NumPy 配列に対応していることは、NumPy のブロー ドキャストに秘密があります(詳しくは「1.5.5 ブロードキャスト」を参照)。ブロー ドキャストの機能により、スカラ値と NumPy 配列での演算が行われると、スカラ値 と NumPy 配列の各要素どうしで演算が行われます。”
      • NumPy便利！
  • 3.2.5 シグモイド関数とステップ関数の比較
    • こういうことを説明することにとても好感を覚える。概念を説明しようとしていることが伝わってくる。
  • 3.2.6 非線形関数
    • “活性化関数の説明では、「非線形関数」「線形関数」という用語がよく登場しま す。そもそも関数は、何かの値を入力すれば何かの値を返す「変換器」です。 この変換器に何か入力したとき、出力が入力の定数倍になるような関数を線形 関数と言います(数式で表すと h(x) = cx。c は定数)。そのため、線形関数 はまっすぐな 1 本の直線になります。一方、非線形関数は、読んで字のごとく (「線形関数に非ず」)、線形関数のように単純な 1 本の直線ではない関数を指し ます。”
      • 分かりやすい。
    • “なぜ線形関数を用いてはならないのでしょうか。それは、線形関数を用いると、 ニューラルネットワークで層を深くすることの意味がなくなってしまうからです。 ”
      • ここ、同じように非線形関数の場合で説明が欲しい。y(x) = c × c × c × x とあるが、c が異なる定数の場合はどうなる？
  • 3.3.3 ニューラルネットワークの内積
    • あくまでの出力は行ベクトルで、ノードは行列になるのか。
  • 3.4 3 層ニューラルネットワークの実装
    • ここも分かりやすいなー。各層の入力と活性化関数の分けて記述し、活性化関数の隠れ層と出力層での役割の違いについても明記していて、概念の共通点と差分が把握しやすい。
    • バイアス項ってノード毎に違うんっだっけ？　←　違う。ノード毎に学習する。
  • 3.5.1 恒等関数とソフトマックス関数
    • 恒等関数の場合はノードって1つにするのかな？複数ある場合、どれを採用すればいいかわからないよね。画像みたいにそれぞれの要素をビットマップの各インデックスや色に対応させてるなら別だけど。
  • 3.5.2 ソフトマックス関数の実装上の注意
    • なるほどなー。式変換てほんと重要だなー。
  • 3.5.3 ソフトマックス関数の特徴
    • “また、ソフトマックス関数の出力の総和は 1 になります。さて、この総和が 1 になるという性質ですが、これはソフトマックス関数の重要な性質です。この性質の おかげでソフトマックス関数の出力を「確率」として解釈することができます。”
      • 実際に確率であるわけではなくて、確率であるとみなすが正しい？
    • “ニューラルネットワークのクラス分類では、一般的に、出力の一番大きいニューロ ンに相当するクラスだけを認識結果とします。そして、ソフトマックス関数を適用し ても、出力の一番大きいニューロンの場所は変わりません。そのため、ニューラル ネットワークが分類を行う際には、出力層のソフトマックス関数を省略することがで きます。実際の問題では、指数関数の計算は、それなりにコンピュータの計算が必要になるので、出力層のソフトマックス関数は省略するのが一般的です。”
      • そーなんだ！確かに分類したいだけなら数値要らないしなー。
  • 3.6.1 MNIST データセット
  • 3.6.2 ニューラルネットワークの推論処理
    • 学習済みのモデルを使うのであまり実感はわかないかも。でも、最終形を先に示すという意味ではいいのかも。
  • 3.6.3 バッチ処理
    • NumPyの素晴らしさが分かってきた。これは便利だなー。

個人的には活性化関数を明示してるのが分かりやすいなーと思いました。Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズで単純パーセプトロンを読んだ際はよくわからなかったので。ただ、5章 誤差逆伝播法 まで読むとニューラルネットワークでは活性化関数は意識するの当然なんだと思ったりもしました。そもそも活性化関数レイヤとして実装するので。

次回はゼロから作るDeep Learning 4章 ニューラルネットワークの学習 - n3104のブログです。

悪いヤツほど出世する

悪いヤツほど出世する

悪いヤツほど出世する

なんとなくネットで見かけて、アマゾンの説明とレビューが良さげだったので読んでみました。レビューの通りで「なるほどねー」とか「そうだよねー」と言いたくなる感じの内容で、若干くどいというのもその通りだと思いましたが、良書だと思いました。

内容としてはリーダー神話は神話であって現実とは異なるということについてひたすらエビデンスを示しながら解説し、読者にはその前提に基づいて行動することを勧めていました。つまり、リーダー神話に存在するようなリーダーはほぼ実在せず、現実のリーダーが嘘をついてもそれほど罰せられることもないので、リーダーシップ教育産業の言葉に惑わされないように気を付けよという内容でした。

自伝とかリーダーシップ？に関する本は多少なりとも読んでいて、ほんとにそんな理想論でうまくいくのかなー？と以前から思っていたので、そういう意味ではとてもスッキリする本でした。

ゼロから作るDeep Learning 2章 パーセプトロン

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

最近、ゼロから作るDeep Learningを読んでます。現時点で4章まで読み終えてますが、ほんと読みやすいと思います。筆者が分かりやすく伝えようとしている熱意を感じる気がしていて、この方が他の書籍も出されたら是非読んでみたいと思ってます。

で、今回は2章 パーセプトロンです。読み終えてからエントリーを書くでもいいかなと思ってたいたのですが、手元のメモのボリュームが結構増えたこともありますし、この本の読書会もやってるのでそのメンバー向けに共有する意味でも、章ごとにエントリーを書こうかなと思いました。

ということで、以下2章に関するメモです。

  • 2.1 パーセプトロンとは
    • “本書では、0 を「信号を流さない」、1 を「信号を流す」に対応させて記述します。”
  • 2.3.3 重みとバイアスによる実装
    • “ここで −θ をバイアス b と命名しましたが”
      • (2.1) 式においてθを閾値としていたが、(2.2) 式においては 0 を敷居としており、b を右辺に移行すると -b となるので前述のように説明している模様。
  • 2.4.2 線形と非線形
    • “パーセプトロンの限界は、このように 1 本の直線で分けた領域だけしか表現できな い点にあります。図2-8 のようなクネッとした曲線をパーセプトロンでは表現できな いのです。” -> 2.5 多層パーセプトロンならできる。
    • “線形・非線形という言葉は機械学習の分野でよく 耳にしますが、イメージとしては図2-6 や図2-8 のようなものを頭に浮かべることが できます。”
      • 線形性とは違う認識でいい？線形=直線=1次関数で非線形は二次関数以上。　←　3.2.6 非線形関数に説明があるように線形関数は直線でいい。一方で非線形関数は二次関数だけでなくシグモイド関数やステップ関数もある。
  • 2.6 NAND からコンピュータへ
    • “コンピュータの内部ではとても複雑な処理を行っているように思えますが、実は (驚くかもしれませんが)NAND ゲートの組み合わせだけで、コンピュータが行う処 理を再現することができるのです。”
    • “理論上 2 層のパーセプトロンであればコンピュータを作 ることができる、と言えます。というのも、2 層のパーセプトロン(正確には活性化 関数に非線形なシグモイド関数を用いたもの:詳細は次章を参照)を用いれば、任意 の関数を表現可能であることが証明されています。しかし、2 層のパーセプトロンの 構造で、適切な重みを設定してコンピュータを作るとなると、それはとても骨の折れ る作業になるでしょう。”
      • すげーな。。

2章に関してはあまりメモがなかったですね、そういえば。。そもそも2章は分量少ないですし、Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズについても別途読書会を実施していて、そちらでパーセプトロンについては勉強してたので、別の切り口で説明していて理解が深まったという感じでした。

次回はゼロから作るDeep Learning 3章 ニューラルネットワーク - n3104のブログです。